常见导数
(e−x)′=−e−x
(−e−x)′=e−x
(arctanx)′=1+x21

常见函数公式
(eax)′=aeax
e−x=(ex)−1=ex1
f′(x)dx=df(x)
∫xadx=a+1xa+1+C
ln(ab)=ln(a)+ln(b)
lnax=xlna
ln1=0,lne=1
lne1=ln1e−1=ln1+lne−1=0+−1lne=−1
lna1=−lna
等比数列
Sn=1−qa1(1−qn)
S∞=1−qa1(∣q∣<1,n→∞)
常见积分
分部积分法
∫uv′dx=uv−∫u′vdx(u/v为x的函数)
∫abuv′dx=(uv)∣ab−∫abu′vdx
基本概念
A∪B=B∪A,AB=BA
0=P(∅)
1=P(A)+P(Aˉ)
1=P(A∣B)+P(Aˉ∣B)
P:事件概率 FX(x)=P{X<x},∫abfX(x)dx=P{a≤X<b}
f:(概率)密度函数 fX(x)=dxdFX(x)
F:(累积)分布函数 FX(x)=∫−∞xfX(x)dx
全集: Ω=∅
联合(累积)分布函数:F(x,y)
联合(概率)密度函数:f(x,y)
边缘密度函数:fX(x)=∫−∞+∞f(x,y)dy ,X取固定值时Y的所有概率的和
X,Y独立:fX(x)⋅fY(y)=fX,Y(x,y)或FX(x)⋅FY(y)=FX,Y(x,y)
一言第一定理/全概率:P(A)=P(AB)+P(ABˉ)
条件概率:P(A∣B)=P(B)P(AB)
条件概率密度:fY∣X(y∣x)=fX(x)f(x,y)
AB事件独立:P(AB)=P(A)P(B)
容斥原理:P(A+B)=P(A)+P(B)−P(AB)
德摩根律/对偶律:Aˉ∪Bˉ=AB,AˉBˉ=A∪B
贝叶斯公式:P(A∣B)=P(B)P(B∣A)P(A)
泰勒展开:ex=1+1!x1+2!x2+⋅⋅⋅
切比雪夫不等式:ε≥0,P{∣X−EX∣<ε}≥1−ε2DX
卷积公式:fX+Y=∫−∞+∞f(x,z−x)dx
中心极限定理
和趋于正态分布
limn→∞P(nσ∑Xi−nμ<x)=2π1∫−∞xe−2t2=ϕ(x)
全概率公式 advanced
前提:B1/B2/Bi互不相交且和为Ω
P(A)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+⋅⋅⋅+P(A∣Bi)P(Bi)
P(A)=P(AB1)+P(AB2)+⋅⋅⋅+P(ABi)
矩(描述数据特征的东西)
中心矩:中心化的矩
把X中心化:X−EX
p阶(原点)矩:E(Xp)
p阶中心矩:E((X−EX)p)
数学期望(一阶原点矩)
p(x)为X的概率密度函数
离散型随机变量 EX=∑x(xp(x))
连续型随机变量 EX=∫−∞+∞xp(x)dx
Eg(X)=∫−∞+∞g(x)p(x)dx
Eg(X,Y)=∫∫g(x,y)f(x,y)dxdy
E(X+Y)=EX+EY
E(aX)=aEX
X,Y独立:E(XY)=(EX)(EY)
方差D()/Var()(二阶中心矩)
DX=E((X−EX)2)=E(X2)−(EX)2
D(X+Y)=D(X)+2Cov(X,Y)+D(Y)
D(X−Y)=D(X)−2Cov(X,Y)+D(Y)
D(cX)=c2DX
协方差(二阶交叉中心矩)
X,Y独立:Cov(X,Y)=0
Cov(X,Y)=E((X−EX)(Y−EY))=E(XY)−(EX)(EY)
Cov(X+Z,Y)=Cov(X,Y)+Cov(Z,Y)
Cov(X,Y+Z)=Cov(X,Y)+Cov(X,Z)
Cov(aX,Y)=aCov(X,Y)
Cov(X,aY)=aCov(X,Y)
相关系数:ρXY=D21(X)D21(Y)Cov(X,Y)
参数估计
X:样本均值
s2:样本方差
样本(无偏)方差 s2=n−1∑(Xi−Xˉ)2
样本一阶矩:X=n∑Xi
样本p阶矩:n∑Xip
点估计
矩估计
思想:用样本矩代替总体矩
- 找到需要估计的总体矩
- 用样本生成相同的矩
极大似然估计
求出最容易得出这个样本的参数
似然函数L():每个样本对应概率密度的乘积
求出L()的最大值
def L(参数组合) -> 样本概率
max(L())
例:练习册 第7章 第2题
L(λ)=i=1∏n(e−λ⋅xi!λxi)=i=1∏ne−λ⋅i=1∏nλxi⋅i=1∏nxi!1=e−nλ⋅λ∑i=1nxi⋅i=1∏nxi!1
ℓ(λ)=ln(e−nλ⋅λ∑i=1nxi⋅i=1∏nxi!1)=lne−nλ+lnλ∑i=1nxi+lni=1∏nxi!1=−nλ+i=1∑nxi⋅lnλ−i=1∑nlnxi!
∂λ∂ℓ(λ)=−n+∑i=1nxi⋅λ1=0
λ=n1∑i=1nxi=xˉ
置信区间/(正态分布的)区间估计
用矩估计或极大似然估计对总体均值做估计是不准确的
这个估计值与总体真实值很难完全相等
因此引入区间估计,区间估计可以估计出一个范围,使得总体均值落在这个区间的概率是比方说95%
def 区间估计(样本值, 置信度: 1-α) -> 置信区间
要使得 EX−aDX→EX+aDX区间的概率为95%
问a=?
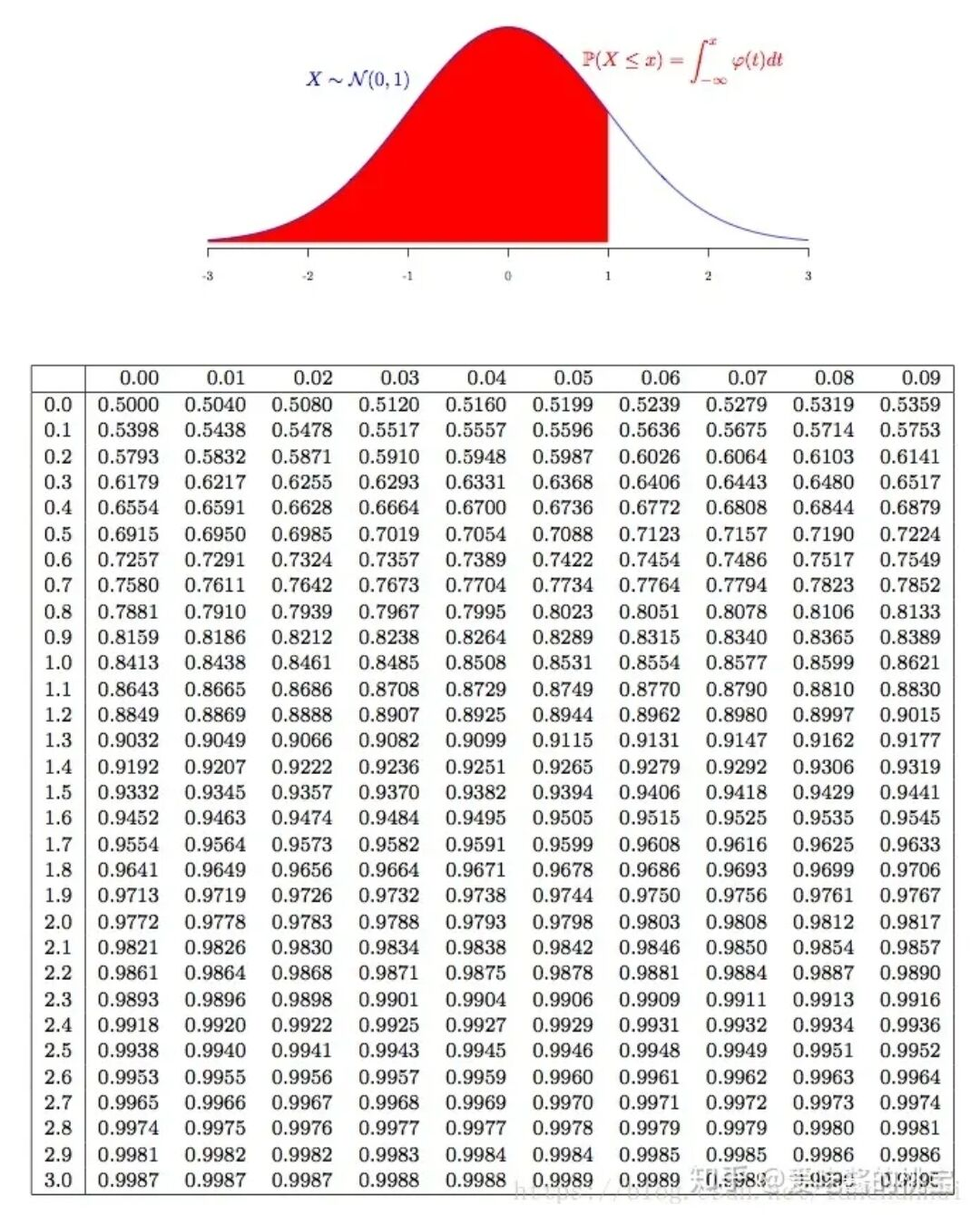
Φ(a)−0.5=20.95
假设检验/显著性检验
> 你猜猜我喝奶茶的时候能不能分辨出它做的时候是先放的奶再放的茶还是先放的茶后放的奶?
< 不能
> 是,Fisher就是偷听奶茶店对话提出了假设检验
奶茶:MT
茶奶:TM
你现在有10杯配好的饮料,给我喝
然后我说是MT还是TM
假设我具备分辨MT与TM的能力
那我对这10杯的判断应该全对ncorrect=10
各种分布
二项分布(伯努利分布) B(n,p)
两点分布(0-1分布) B(n=1,p)
EX=np
DX=np(1−p)
X∼B(n1,p),Y∼B(n2,p)且独立,X+Y∼B(n1+n2,p)
均匀分布 U(a,b)
F(x)=b−ax−a,a≤x≤b
f(x)=b−a1,a<x<b
EX=2a+b
DX=12(a−b)2
指数分布 Exp(θ)
f(x)=θ1e−θx,x>0
F(x)=1−e−θx,x>0
正态分布 Norma(μ,σ2)
标准正态分布Z=N(0,1)
N(μ,σ2)+c=N(μ+c,σ2)
cN(μ,σ2)=N(cμ,c2σ2)
X∼N(a,b2)<=>bX−a∼N(0,1)
f(x)=2πσ1e−2σ2(x−μ)2
独立即可加:N (μ1,σ12)+N(μ2,σ22)=N(μ1+μ2,σ12+σ22)
Fisher定理:正态分布的样本均值和样本方差相互独立
正态分布样本均值的分布:X∼N(μ,nσ2)
正态分布样本方差的分布:σ2(n−1)s2∼χ2(n−1)
ϕ(?):正态曲线从−∞积分到μ+?的值
泊松分布 Poi(λ)
P{X=k}=k!λke−λ,k=0,1,2⋯
EX=DX=λ
卡方分布 χ2(n: 自由度)
n个标准正态分布N(0,1)的平方之和的分布
数学语言:
设 Z1,Z2,⋯,Zn 互相独立且服从 N(0,1)
则称随机变量X=Z12+Z22+⋯+Zn2
服从自由度为 n 的卡方分布, 记作 X∼χ2(n)
Z12+Z22+⋯+Zn2∼χ2(n)
均方:平方和除以n
F分布 F(n,m)
F(n,m)=χ2(m)/mχ2(n)/n
m个标准正态分布均方标准正态分布平方=F(1,m)
nZ12+Z22+⋯+Zn2/mW12+W22+⋯+Wm2∼F(n,m)whereZi,Wi∼N(0,1)i.i.d
t分布
Z/nW12+W22+⋯+Wn2∼t(n)
