常用导数
未分类
(kx)′=k
(μ+1xμ+1)′=xμ,μ=−1
(ln∣x∣)′=x1
(lnaax)′=ax
常数的求导法则
常数′=0
幂函数的求导法则
(xμ)′=μxμ−1
三角函数的求导法则
(sinx)′=cosx
(cosx)′=−sinx,
(−cosx)′=sinx
(tanx)′=(secx)2=(cosx)21,
(cotx)′=−(cscx)2,
(−cotx)′=(cscx)2=(sinx)21
(secx)′=secxtanx,
(cscx)′=−cscxcotx,
(−cscx)′=cscxcotx
指数函数的求导法则
(ax)′=axlna,(a>0,a=1)
(ex)′=ex
对数函数的求导法则
(logax)′=xlna1,(a>0,a=1)
(lnx)′=x1
反三角函数的求导法则
(arcsinx)′=1−x21
(arccosx)′=−1−x21
(arctanx)′=1+x21
(arccotx)′=−1+x21
导数的定义
函数 f(x) 在 x 处的导数:
limh→0hf(x+h)−f(x)
导数的几何意义:函数图像 在 该点 的 切线
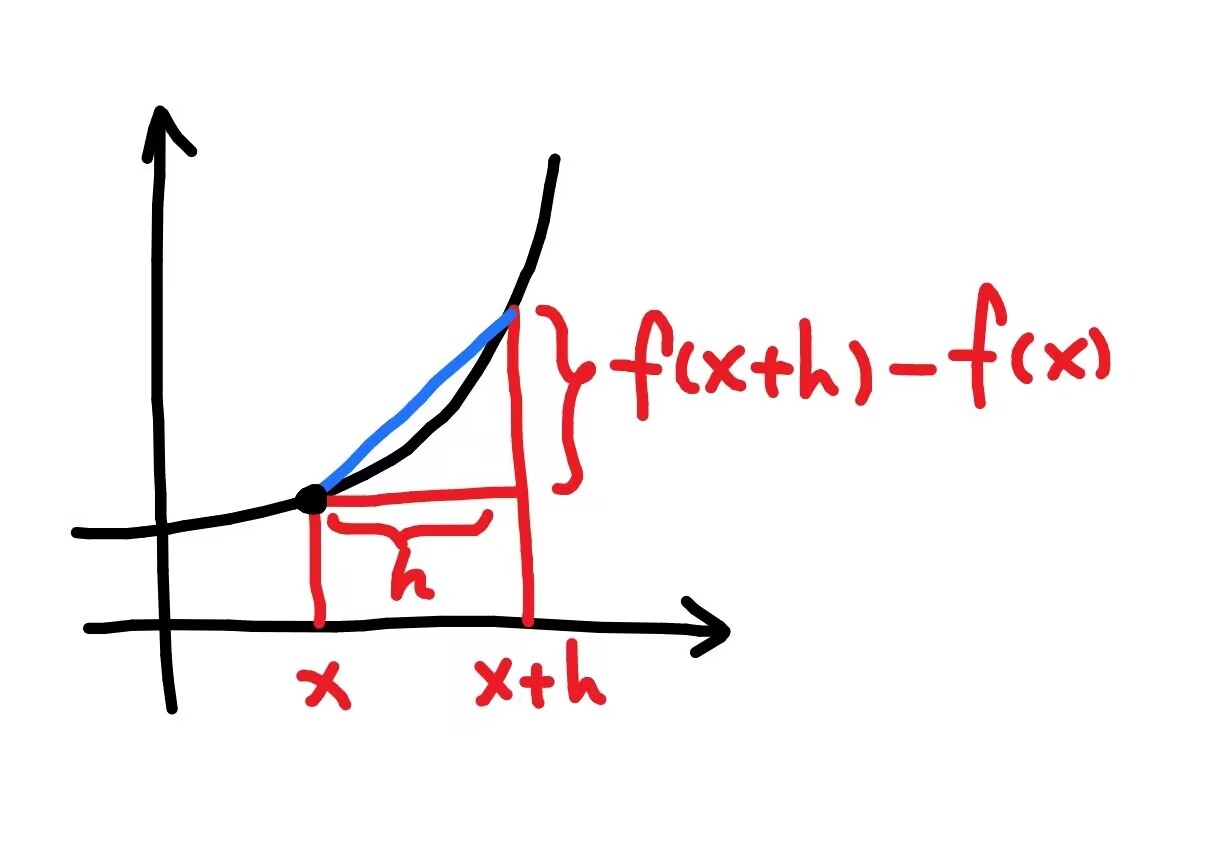
现在给定 x 和 h,要求蓝线的斜率,
蓝线的斜率 是这个 直角三角形 的 高 除以 底边长
现在考虑以下的极限过程:
x+h 慢慢向 x 逼近,也就是 h 慢慢向 0 逼近,这条蓝线的斜率就会慢慢接近切线斜率,也就是 x 处的导数。
随着 h 慢慢趋近 0,蓝线会越来越接近切线。
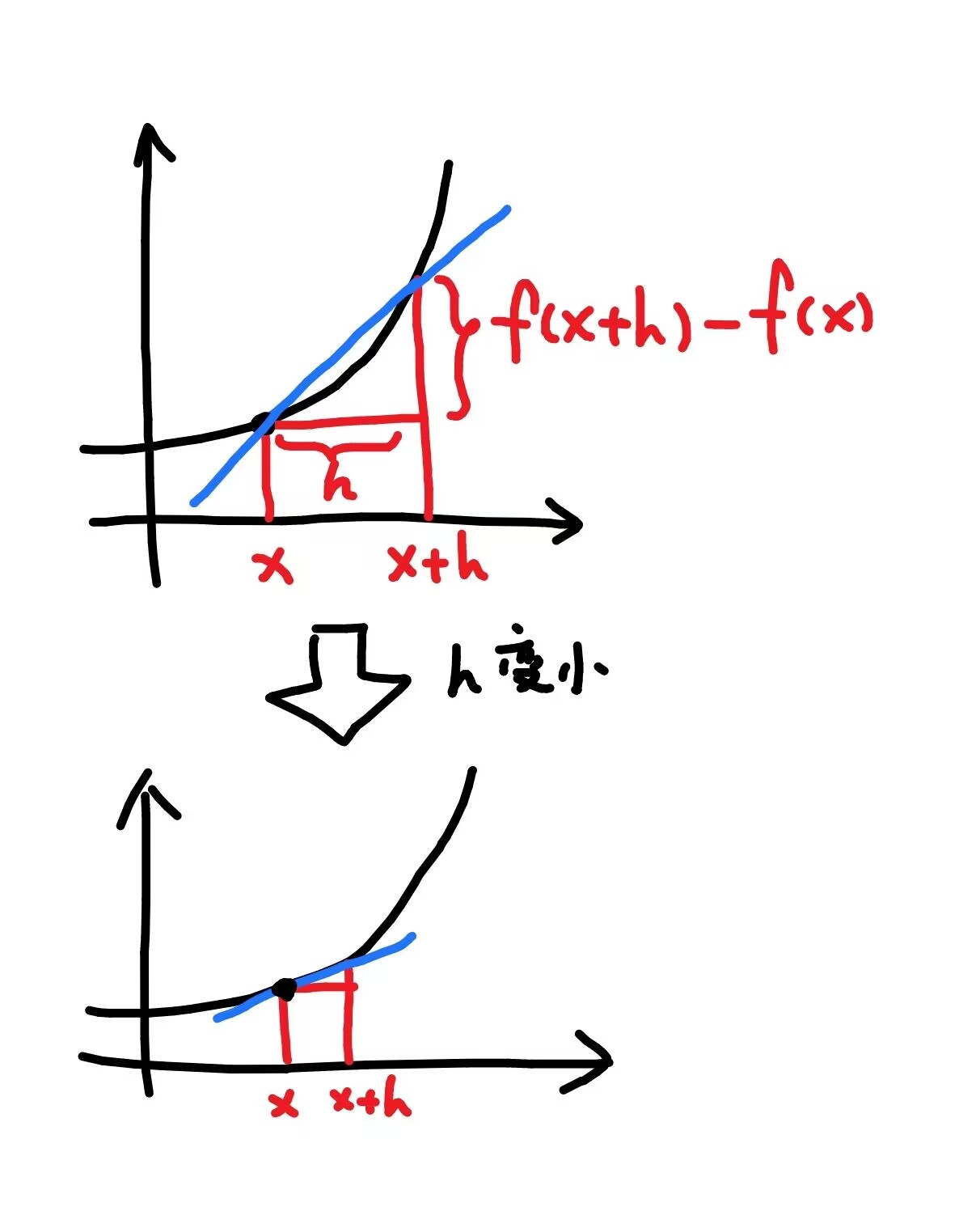
这条蓝色线称作割线。
导数定义的整体思路是:用割线逼近切线。
积分式求导
dxd∫常数xf(t)dt=f(x)
函数 和,差,积,商 求导
(f±g)′=f′±g′
(fg)′=f′g+fg′
(gf)′=g2f′g−fg′
链式法则
dBdA=dCdA⋅dBdC

