手撸 K近邻 算法

可用的库为 NumPy、Matplotlib，不能使用 sklearn 库，然后将该算法用于鸢尾花问题分类。

要求使用三种距离函数：欧氏距离 、 曼哈顿距离 与 夹角余弦。

要求对 K 设置三种不同数值，对比分析三种不同距离的不同K值何种效果最好。

K近邻算法视频介绍：https://www.bilibili.com/video/BV1vA4y1o72F/?p=1

摘要

KNN算法是一种基于实例的监督学习算法，用于解决分类和回归问题。在KNN算法中，给定一个未知样本，首先找到与该样本最相似的K个训练样本，然后根据这K个训练样本的类别信息，进行分类或回归预测。

KNN算法的核心思想是“近朱者赤，近墨者黑”。也就是说，与未知样本相似的训练样本，往往具有相同的类别信息。因此，在KNN算法中，找到与未知样本最相似的K个训练样本，可以有效地预测该未知样本的类别或数值。

概述

KNN算法的具体实现过程包括以下几个步骤：

1. 选择距离度量方法，如欧氏距离、曼哈顿距离等。
2. 给定一个未知样本，计算该样本与训练集中每个样本之间的距离。
3. 根据距离从小到大对训练集中的样本进行排序，选取与未知样本最近的K个样本。
4. 根据K个样本的类别信息，进行分类或回归预测。对于分类问题，可以采用多数投票等方法决定样本的类别；对于回归问题，可以采用平均值等方法预测样本的数值。

在本实验中，应该没有涉及到回归问题。

我的工作

为了尽量减少对第三方库的依赖，在本实验中，我仅使用 Matplotlib 库来绘制图表。

需要导入的库如下：

from dataclasses import dataclass
from math import sqrt
import csv
from typing import Callable
import matplotlib.pyplot as plt

下载鸢尾花数据集

数据集下载地址：https://archive.ics.uci.edu/dataset/53/iris

下载后将压缩包中的 iris.data 文件放到工作目录下。

该数据集文件中包含150个样本，每个样本包含4个特征和1个类别信息。其中，4个特征分别为花萼长度、花萼宽度、花瓣长度和花瓣宽度，类别信息包含3种鸢尾花的类别，分别为山鸢尾、变色鸢尾和维吉尼亚鸢尾。

读取数据集

该数据集为标准的 csv 格式文件，使用 python 内置的 csv 库解析即可。

def load_iris(data_file_path: str) -> list[Iris]:
    """加载鸢尾花数据集"""
    with open(data_file_path, newline='') as f:
        iris_list: list[Iris] = []
        for row in csv.reader(f):
            if len(row) != 5:
                continue
            iris_list.append(Iris(float(row[0]), float(row[1]), float(row[2]), float(row[3]), row[4]))
        return iris_list

在读取数据集时，我将每个样本的特征和类别信息封装到了 Iris 类中，方便后续的处理。

@dataclass
class Iris:
    """鸢尾花"""
    sepal_length: float  # 花萼长度
    sepal_width: float  # 花萼宽度
    petal_length: float  # 花瓣长度
    petal_width: float  # 花瓣宽度
    clazz: str  # 类别

定义距离算法

在KNN算法中，距离度量方法是一个重要的参数，它决定了样本之间的相似度。常用的距离度量方法包括欧氏距离、曼哈顿距离、夹角余弦等。

欧氏距离

def euclidean_distance(x1: list[float], x2: list[float]) -> float:
    """欧氏距离"""
    distance = []
    for i in range(len(x1)):
        distance.append((x1[i] - x2[i]) ** 2)
    return sqrt(sum(distance))

曼哈顿距离

def manhattan_distance(x1: list[float], x2: list[float]) -> float:
    """曼哈顿距离"""
    distance = []
    for i in range(len(x1)):
        distance.append(abs(x1[i] - x2[i]))
    return sum(distance)

夹角余弦

def cosine_distance(x1: list[float], x2: list[float]) -> float:
    """余弦距离"""
    dot_product = sum([x1[i] * x2[i] for i in range(len(x1))])
    mod_x1 = sqrt(sum([x ** 2 for x in x1]))
    mod_x2 = sqrt(sum([x ** 2 for x in x2]))
    return 1 - dot_product / (mod_x1 * mod_x2)

封装距离算法

为了使得这些距离算法适配该实验的数据集，我将距离算法函数进行进一步的封装，使得函数的参数为两个 Iris 对象，返回值为两个样本之间的距离。

def distance_for_iris(ori_func: Callable[[list[float], list[float]], float]) -> Callable[[Iris, Iris], float]:
    """针对鸢尾花的距离函数封装"""

    def distance(iris1: Iris, iris2: Iris) -> float:
        return ori_func(
            [iris1.sepal_length, iris1.sepal_width, iris1.petal_length, iris1.petal_width],
            [iris2.sepal_length, iris2.sepal_width, iris2.petal_length, iris2.petal_width]
        )

    return distance

定义 KNN 分类器

用一个类来封装 KNN 分类器，把相关的参数和方法封装在一起，方便使用。

class KNNClassifier:
    """KNN分类器"""

    def __init__(self, _train_set: list[Iris], _k: int, _distance_function: Callable[[Iris, Iris], float]):
        self.train_set = _train_set
        self.k = _k
        self.distance_function = _distance_function

    def classify(self, _iris: Iris) -> str:
        """分类"""
        # 计算距离 [(距离, 类型)]
        distances: list[(float, str)] = []
        for train_iris in self.train_set:
            distances.append((self.distance_function(_iris, train_iris), train_iris.clazz))
        distances.sort(key=lambda x: x[0])  # 排序

        # 统计最近 k 个样本的类型 {类型: 计数}
        count: dict[str, int] = {}
        for i in range(self.k):
            count[distances[i][1]] = count.get(distances[i][1], 0) + 1
        return max(count, key=lambda x: count[x])  # 返回最多的类别

开始分类

iriss: list[Iris] = load_iris('iris.data')

distance_function: dict[str, Callable[[Iris, Iris], float]] = {
    '欧氏距离': distance_for_iris(euclidean_distance),
    '曼哈顿距离': distance_for_iris(manhattan_distance),
    '夹角余弦': distance_for_iris(cosine_distance)
}

train_size: int = int(len(iriss) * 0.8)
train_set: list[Iris] = iriss[:train_size]
test_set: list[Iris] = iriss[train_size:]

k_list: list[int] = [i for i in range(1, 10, 2)]

for distance_name, distance_func in distance_function.items():
    accuracy_list = []
    for k in k_list:
        knn = KNNClassifier(train_set, k, distance_func)
        correct_count = 0
        for iris in test_set:
            if knn.classify(iris) == iris.clazz:
                correct_count += 1
        accuracy: float = correct_count / len(test_set)
        print(f'K= {k:<2}', f'{distance_name:<6}', f'正确率：{accuracy:.2%}')
        accuracy_list.append(accuracy)

    # 计算最佳K值
    max_accuracy = max(accuracy_list)
    max_index = accuracy_list.index(max_accuracy)
    print(f'最佳K值：{k_list[max_index]}')

    # 绘制 分类正确率曲线 和 最佳K值
    plt.plot(k_list, accuracy_list, label=distance_name)
    plt.plot(k_list[max_index], max_accuracy, 'ro')

# 添加图例和标签
plt.legend()
plt.xlabel('K值')
plt.ylabel('准确率')
plt.title('多个距离函数对鸢尾花数据集使用KNN分类器的准确率')

# 显示图形
plt.show()

如果中文显示有问题，要在绘制图像前设置中文字体。

plt.rcParams['font.family'] = 'Microsoft YaHei'

运行结果

K= 1  欧氏距离   正确率：83.33%
K= 3  欧氏距离   正确率：76.67%
K= 5  欧氏距离   正确率：80.00%
K= 7  欧氏距离   正确率：80.00%
K= 9  欧氏距离   正确率：76.67%
最佳K值：1
K= 1  曼哈顿距离  正确率：73.33%
K= 3  曼哈顿距离  正确率：76.67%
K= 5  曼哈顿距离  正确率：80.00%
K= 7  曼哈顿距离  正确率：76.67%
K= 9  曼哈顿距离  正确率：80.00%
最佳K值：5
K= 1  夹角余弦   正确率：86.67%
K= 3  夹角余弦   正确率：83.33%
K= 5  夹角余弦   正确率：86.67%
K= 7  夹角余弦   正确率：86.67%
K= 9  夹角余弦   正确率：86.67%
最佳K值：1

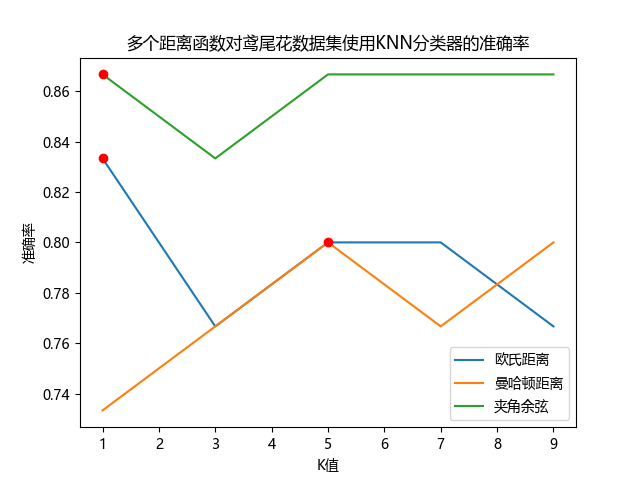
可以发现，使用夹角余弦距离的KNN分类器的准确率最高，达到了86.67%。

使用欧氏距离时，K=1时准确率最高，为83.33%；使用曼哈顿距离时，K=5,9时准确率最高，达到了80.00%；使用夹角余弦时，K=1,5,7,9时准确率最高，为86.67%。

总结与展望

KNN算法具有简单、直观、易于理解的特点，并且适用于各种类型的数据。但是，KNN算法的主要缺点是计算复杂度高，对于大规模数据集，需要消耗大量的计算资源和时间。此外，KNN算法还对数据集中的噪声和异常值比较敏感，容易出现过拟合和欠拟合等问题。因此，在应用KNN算法时，需要根据实际情况进行参数设置和模型优化，以达到更好的分类或回归效果。

为了减少第三方库的调用，这次学习参考了视频和各种资料，还咨询了万能的群友，感谢大家的帮助！

希望在未来的学习中，我能更好地理解更多机器学习算法，即使未来可能不需要自己实现算法，也能更好地理解算法的原理，以便构建更好的模型。

完整代码，Python 3.10.10

from dataclasses import dataclass
from math import sqrt
import csv
from typing import Callable
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams['font.family'] = 'Microsoft YaHei'


@dataclass
class Iris: 
    """鸢尾花"""
    sepal_length: float  # 花萼长度
    sepal_width: float  # 花萼宽度
    petal_length: float  # 花瓣长度
    petal_width: float  # 花瓣宽度
    clazz: str  # 类别


def load_iris(data_file_path: str) -> list[Iris]:
    """加载鸢尾花数据集"""
    with open(data_file_path, newline='') as f:
        iris_list: list[Iris] = []
        for row in csv.reader(f):
            if len(row) != 5:
                continue
            iris_list.append(Iris(float(row[0]), float(row[1]), float(row[2]), float(row[3]), row[4]))
        return iris_list


def euclidean_distance(x1: list[float], x2: list[float]) -> float:
    """欧氏距离"""
    distance = []
    for i in range(len(x1)):
        distance.append((x1[i] - x2[i]) ** 2)
    return sqrt(sum(distance))


def manhattan_distance(x1: list[float], x2: list[float]) -> float:
    """曼哈顿距离"""
    distance = []
    for i in range(len(x1)):
        distance.append(abs(x1[i] - x2[i]))
    return sum(distance)


def cosine_distance(x1: list[float], x2: list[float]) -> float:
    """余弦距离"""
    dot_product = sum([x1[i] * x2[i] for i in range(len(x1))])
    mod_x1 = sqrt(sum([x ** 2 for x in x1]))
    mod_x2 = sqrt(sum([x ** 2 for x in x2]))
    return 1 - dot_product / (mod_x1 * mod_x2)


def distance_for_iris(ori_func: Callable[[list[float], list[float]], float]) -> Callable[[Iris, Iris], float]:
    """针对鸢尾花的距离函数封装"""

    def distance(iris1: Iris, iris2: Iris) -> float:
        return ori_func(
            [iris1.sepal_length, iris1.sepal_width, iris1.petal_length, iris1.petal_width],
            [iris2.sepal_length, iris2.sepal_width, iris2.petal_length, iris2.petal_width]
        )

    return distance


class KNNClassifier:
    """KNN分类器"""

    def __init__(self, _train_set: list[Iris], _k: int, _distance_function: Callable[[Iris, Iris], float]):
        self.train_set = _train_set
        self.k = _k
        self.distance_function = _distance_function

    def classify(self, _iris: Iris) -> str:
        """分类"""
        # 计算距离 [(距离, 类型)]
        distances: list[(float, str)] = []
        for train_iris in self.train_set:
            distances.append((self.distance_function(_iris, train_iris), train_iris.clazz))
        distances.sort(key=lambda x: x[0])  # 排序

        # 统计最近 k 个样本的类型 {类型: 计数}
        count: dict[str, int] = {}
        for i in range(self.k):
            count[distances[i][1]] = count.get(distances[i][1], 0) + 1
        return max(count, key=lambda x: count[x])  # 返回最多的类别


# 加载鸢尾花数据集
iriss: list[Iris] = load_iris('iris.data')
# 距离函数
distance_function: dict[str, Callable[[Iris, Iris], float]] = {
    '欧氏距离': distance_for_iris(euclidean_distance),
    '曼哈顿距离': distance_for_iris(manhattan_distance),
    '夹角余弦': distance_for_iris(cosine_distance)
}

# 划分训练集和测试集
train_size: int = int(len(iriss) * 0.8)
train_set: list[Iris] = iriss[:train_size]
test_set: list[Iris] = iriss[train_size:]

# K值
k_list: list[int] = [i for i in range(1, 10, 2)]

# 测试
for distance_name, distance_func in distance_function.items():
    accuracy_list = []
    for k in k_list:
        knn = KNNClassifier(train_set, k, distance_func)
        correct_count = 0
        for iris in test_set:
            if knn.classify(iris) == iris.clazz:
                correct_count += 1
        accuracy: float = correct_count / len(test_set)
        print(f'K= {k:<2}', f'{distance_name:<6}', f'正确率：{accuracy:.2%}')
        accuracy_list.append(accuracy)

    # 计算最佳K值
    max_accuracy = max(accuracy_list)
    max_index = accuracy_list.index(max_accuracy)
    print(f'最佳K值：{k_list[max_index]}')

    # 绘制 分类正确率曲线 和 最佳K值
    plt.plot(k_list, accuracy_list, label=distance_name)
    plt.plot(k_list[max_index], max_accuracy, 'ro')

# 添加图例和标签
plt.legend()
plt.xlabel('K值')
plt.ylabel('准确率')
plt.title('多个距离函数对鸢尾花数据集使用KNN分类器的准确率')

# 显示图形
plt.show()